Q1. 축약형(2단계) 단계 예측의 잔차는?
e^IV=Y−β^IVT2단계의 .resid에서 얻는 잔차와 동일하지 않음을 조심할 것!
Y−β^IVT^ 💡
축약형 단계 예측의 잔차를 이용하여 도구변수 추정값에 대한 표준오차를 계산할 수 있다.SE(β^IV)=β^z,1stσ(Z)nσ(ϵ^IV)코드 예시 및 결과
Z= df["prime_eligible"]
T= df["prime_card"]
n = len(df)
e_iv = df["pv"] - iv_regr.predict(df)
compliance = np. cov(T, Z)[0, 1]/Z.var()
se = np.std(e_iv)/(compliance*np.std(Z)*np.sqrt(n))
print("SE IV:", se)
print ("95% CI:", [late - 2*se, late +2*se])
# 결과
SE IV: 80.52861026141942
95% C:I [596.6401590115549, 918.7546000572327]
추가로, linearmodels에서 2SLS 모듈을 사용하면, 결과 재확인이 가능하다.
코드 예시 및 결과
from linearmodels import IV2SLS
formula ='pv ~1+[prime_card ~prime_eligible]'
iv_model = IV2SLS. from_formula(formula, df).fit(cov_type="unadjusted")
iv_model.summary.tables[1]
 앞선 코드와 동일한 표준오차
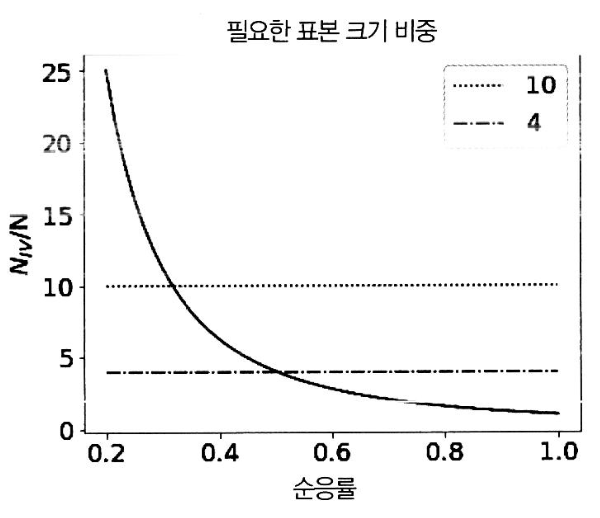
앞선 코드와 동일한 표준오차 Q2. 표준오차 공식이 불응 실험에서 마주하는 어려움을 일정 부분 설명해줄 수 있는 이유?
SE(β^IV)=β^z,1stσ(Z)nσ(ϵ^IV)- 이항분포 표준편차의 최댓값 = 0.5
- σ(Z)=n⋅p⋅(1−p)
이항분포 표준편차의 최댓값이 0.5인 이유?
표준편차
σ(Z)가 최대가 되려면
p⋅(1−p)가 최대가 되어야 한다.
이항 변수의 경우,
p⋅(1−p)는
p = 0.5일 때 최대값을 가진다.
11.8 통제변수와 도구변수 추가
Q1. 프라임 신용카드 데이터
- 프라임 신용카드 데이터
- 기본 변수 :
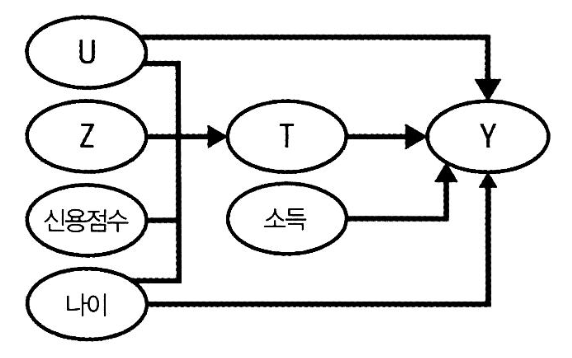
처치변수(T) 도구변수(Z) 결과변수(Y) 위 변수들의 개념과 특징이 헷갈린다면!
- 처치변수(T) : 실험이나 연구에서 어떤 처치를 받았는지, 인과관계에서 원인 역할을 하는 변수
- 도구변수(Z) : 실험이나 연구에서 처치변수와 결과변수 간의 인과관계를 추정하기 위해 사용하는 변수
- 결과변수(Y) : 실험이나 연구에서 처치에 대한 어떤 결과를 얻었는지, 결과 역할을 하는 변수
- 추가 변수(공변량) :
소득 나이 신용점수
Q2. 2SLS 직접 구현
💡
1단계 : 처치(T)를 도구변수(Z)와 추가 공변량(X)에 회귀
- 예시 :
prime_card ~ prime_eligible + credit_score + income + age
formula 1st = "prime_card ~ prime_eligible + credit_score + income+age"
first_stage =smf.ols(formula_1st, data=df).fit()
💡
2단계 : 결과(Y)를 1단계에서 얻은 처치(T_hat)와 추가 공변량(X)에 회귀
- 예시 :
pu ~ prime_card + income + age (여기서 prime_card는 1단계에서 얻은 적합된 값)
iv_model = smf.ols(
"pu ~prime_card +income +age",
data=df.assign(prime_card=first_stage.fittedvalues)).fit()
Q3. 행렬을 사용한 2SLS 구현
2SLS 직접 구현하면 도구변수 추정값은 얻을 수 있지만 표준오차는 달라지기 때문에, 표준오차를 구하고 싶다면 다음과 같은 과정을 따라해야 한다.
💡
도구 변수 행렬(Z)과 처치 행렬(X)에 추가 공변량(X)을 포함
- 1단계 회귀 :
- 회귀 계산 : Xhat =Z(ZTZ)−1ZTX
계산식 뜯어보기
- (ZTZ) : 도구변수들 간의 상관관계를 나타내는 행렬
- Z(ZTZ)−1 : 위 행렬을 역행렬로 변환하여, 도구변수들 간의 관계를 보정
- ZTX : 도구변수와 처치변수 간의 상관관계를 나타내는 행렬
- Xhat : 이 모든 요소를 결합하여 계산하면, 도구변수를 통해 추정된 처치변수의 예측값을 얻음
- 회귀 계수 추정 :
- 계산 : βiv=(Xhat TXhat )−1Xhat TY
계산식 뜯어보기
- Xhat TXhat : 예측된 처치변수와 그 자신과의 상관관계를 나타내는 행렬
- Xhat TY : 예측된 처치변수와 결과변수 간의 상관관계를 나타내는 행렬
- βiv : 이 모든 요소를 결합하여 계산하면, 처치변수와 결과변수 간의 인과관계를 추정
Z = df[["prime_eligible", "credit_score", "income", "age"]].values
X = df[["prime_card", "income", "age"]].values
Y = df[["pv"]].values
X_hat = Z.dot(np.linalg.inv(Z.T.dot(Z)).dot(Z.T).dot(X))
b_iv = np.linalg.inv(X_hat.T.dot(X_hat)).dot(X_hat.T).dot(Y)
Q4. 표준오차 계산
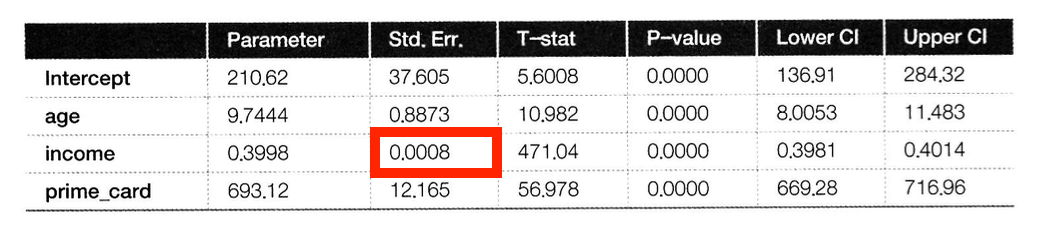
앞서 구한 회귀 계수를 바탕으로 표준오차를 계산한다.
- 오차 추정 :
- Var(β^)=σ2(X^TX^)−1
e_hat_iv = Y - X_.dot(b_iv)
var = e_hat_iv.var() * np.diag(np.linalg.inv(X_hat.T.dot(X_hat)))
np.sqrt(var[1])
Q5. 표본 늘리는 방법 외에도, 표준오차를 줄이는 방법은?
- 1단계의 R2 증가:
- 순응을 잘 예측하는 강력한 도구 변수를 찾는 것.
- 결과(Y)에 영향을 미치지 않으면서 배제 제약을 만족해야 함.
- T에 대한 예측력이 높은 변수 제거:
- 1단계의 오차(잔차)를 줄여 R2를 증가시키기.
- 결과(Y)의 예측력이 높은 변수 추가:
- 결과(Y)의 예측력이 높은 변수를 찾아, 2단계 잔차를 줄이는 것.
💡
2SLS 모델의 성능을 높이는 가장 현실적인 방법은 결과(Y)를 잘 예측하는 변수를 찾는 것.→ 실전에서 도구 변수를 찾는 것은 매우 어렵기 때문.