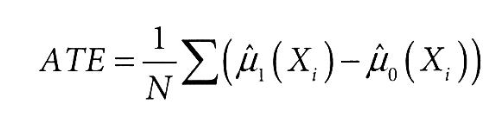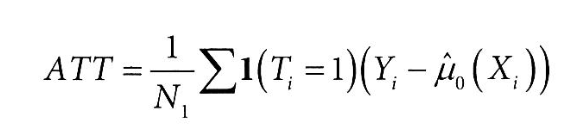[인과추론] 결과 모델로서의 회귀분석, 양수성과 외삽

Q1. 처치의 종류는?

• ATE(Average Treatment Effect) : 평균적인 인과 효과

• ATT(Average Treatment effect on the Treated) : 평균 처치 효과

Q2. 사례를 통해 ATE와 ATT를 비교해볼까?

• 각 집단의 결과값의 평균을 비교한 것이, ATE
treatment group 의 몸무게 감소 평균 - control group 의 몸무게 감소 평균

두 그룹의 평균 차이인 ATE가 인과관계를 증명하진 않음

→ 두 그룹이 완전히 동일하지 않기 때문에 어느 정도의 bias가 생김

→ 따라서, 이론적으로 완벽한 인과관계 효과는 ATE - bias 이고, 이를 ATT라고 함

• ATE에서 bias를 뺀 것이, ATT
이상적인 효과지만 구하기 불가능한 값 (ex. 학생 A 부모의 이혼 유무에 따른 학력 차이를 비교 → 비교가 불가능하니 A와 비슷한 다른 학생과 A를 비교하는 것.)

Q3. 실험 설계자의 목적은?

• ATT가 이상적인 지표지만 구하기 불가능
→ bias를 최대한 줄여 ATE를 ATT에 최대한 가깝게 해야함
→ bias를 최대한 줄이려면, 비교군과 대조군이 거의 동일해야 함

4.5 양수성과 외삽

Q1. 양수성 가정이란?

• 교란변수가 주어졌을 때 처치의 조건부 확률은 (0<P(T∣X)<1)
→ 양수성 가정을 위배해도 식별이 가능하지만, 위험한 외삽을 해야 함

Q2. 외삽이란?

• 원래의 관찰 범위를 넘어서서 다른 변수와의 관계에 기초하여 변수의 값을 추정하는 과정
→ 얻을 수 있는 자료가 한정되어 그 이상의 한계를 넘는 값을 얻고자 할 때 쓰는 방법

Q3. 외삽의 합리적인 유무에 따른 결과는?

• 축복일 경우
💡
중첩이 적은 데이터셋에서 처치 효과를 추정해야 한다고 가정
 
• 공변량 x의 값이 클 때는 대조군이 존재 X
• 공변량 x의 값이 작을 때는 실험군이 존재 X
→ 공변량 공간 전반에 중첩이 있는 결과 추세선이 비슷하면, 약간의 외삽은 문제가 되지 않음

• 저주일 경우
💡
축복일 경우보다, 더 많은 데이터를 수집하여 처치를 무작위로 배정하게 됐다고 가정
 
• 공변량 x가 음수일 때보다 양수일 때 효과가 점점 커짐
→ 처치의 실제 처치효과보다 크게 과소평가하여, 처치효과를 정확히 알 수 없음

Q3. 요약

양수성 가정이 충족되지 않을 경우 회귀분석은 외삽을 통해 해당 가정이 충족되지 않는 영역을 대체하게 됨